What Are Examples of Fourth Order Differential Equations | Step-by-Step Solution

Examples for the fourth order differential equation are,

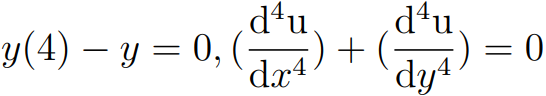
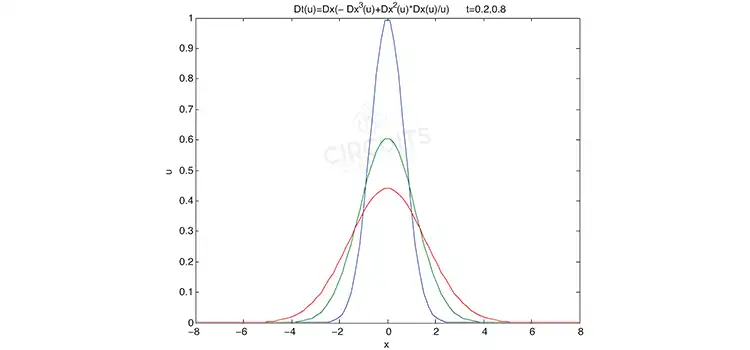
Figure-1: Graph of a fourth-order differential equation.

The degree of the differential equation is the power of the highest-order derivative. Here the original equation is expressed as derivatives such as y’, y”, y”‘, and so on.

How Do You Solve a Fourth-Order Differential Equation

The steps of solving a fourth-order differential equation are illustrated below

Step-1: Write the characteristics equation.

For the equation: y⁴ +y³+y² =0 … (Eqn. 1)

The characteristics equation will be m⁴ +m³+m² =0 … (Eqn. 2)

Step-2: Derive what the characteristics equation is the factor of.

For equation 2, m² (m² +m¹+1)=0 … (Eqn.3)

Step-3: Use the quadratic formula to derive the value of m.

For equation 3, m=0, m=-1/2±ϳ3

Step-4: Finish the solution by solving it for y.

What Are the Four Types of Fourth-Order Differential Equations

The four types of fourth-order differential equations are:

1. Ordinary Differential Equations (ODE)

In mathematics, an ordinary differential equation (often abbreviated as ODE) is an equation that consists of one or more functions of one independent variable and its derivatives. A differential equation is a mathematical expression that contains a function with one or more derivatives.

Example 

y⁴=x⁴+1

2. Partial Differential Equation (PDE)

A partial differential equation is a mathematical expression that contains an unknown function of two or more variables and its partial derivatives concerning these variables. The highest-order derivatives determine the order of a partial differential equation.

Example

∂⁴u/∂t⁴=c^4* (∂⁴u/∂x⁴ )

3. Linear Differential Equation

The linear polynomial equation, which consists of derivatives of numerous variables, defines a linear differential equation. When the function is dependent on variables and the derivatives are partial, it is also referred to as Linear Partial Differential Equation.

Example

(dy/dx)⁴ + Py⁴ = Q 

4. Non-linear Differential Equation

A nonlinear differential equation is not linear in the unknown function and its derivatives. It provides several solutions that might be seen for chaos.

Example

[y⁴(x)]2+y³(x)=f(x³)

What Are the Applications of Fourth-Order Differential Equations?

In real life, fourth-order differential equations are used to compute the movement or flow of electricity, the motion of an object to and fro like a pendulum, and to illustrate thermodynamic ideas. They are also used in medicine to monitor the progression of diseases in graphical form.

Conclusion

Fourth-order nonlinear differential equations occur naturally in models of physical, biological, and chemical phenomena. Such as elasticity, structural deformation, and soil settlement.